신경망 (neural network)
udacity self driving car의 computer vision 부분을 통해 학습한 내용을 정리한 페이지 입니다.
개요
지금까지의 computer vision은 사용자가 알고리즘을 직접 작성하여 도로상황을 판단하였습니다. 그러나 최근 머신러닝과 관련된 이론과 기술이 발달하고, 이를 처리할 수 있는 정도의 컴퓨터 기술이 발달한 덕에 컴퓨터가 다양한 상황을 학습하여 도로 상황을 인식하는 방법을 사용할 수 있게 되었습니다.
신경망
이러한 머신러닝에선 신경망 구조를 이용합니다. 우리 뇌에 있는 뉴런과 같이 입력이 들어오면 그에 따라 어떤 출력을 내보내는지 결정하는 모델을 형상화 한 것입니다. 신경망 구조는 여러가지가 있을 수 있는데, 그중 분류 과정에 사용되는 신경망형태를 통해 알아보도록 하겠습니다.
신경망 - ?
신경망의 기본적인 개념은 방정식을 찾는 것입니다. 직관적으로, 대학교에 합격, 불합격을 예측한다고 합시다. 알고있는 정보는 대학교에 지원한 인원들의 등수와 시험점수입니다. 당연히 등수와 시험점수 둘다 높은경우에 합격하겠지만, 그렇지 않은 경우도 많습니다. 대학 합격에는 시험점수가 중요할 수도 있고 등수가 중요할 수도 있습니다. 이를 표현하기 위해 몇가지 가정을 하도록 하겠습니다.
- 양수일 경우 합격, 음수일경우 불합격으로 예측한다.
- 합격을 예측하기 위해 등수와 시험점수를 그래프로 나타내어, 합격과 불합격을 분류하는 경계를 찾는다.
그럼 해당 정보의 중요도를 숫자로 나타내어 방정식으로 표현해보겠습니다.
\[\begin{aligned} 등수*중요도_{등수}+시험점수*중요도_{시험점수}-편차=y \end{aligned}\]이는 다음 그림과 같은 그래프상에서 직선의 형태로 나타나게 됩니다. 해당 직선보다 위에 있으면 합격, 아래에 있으면 불합격이라 유추할 수 있습니다.
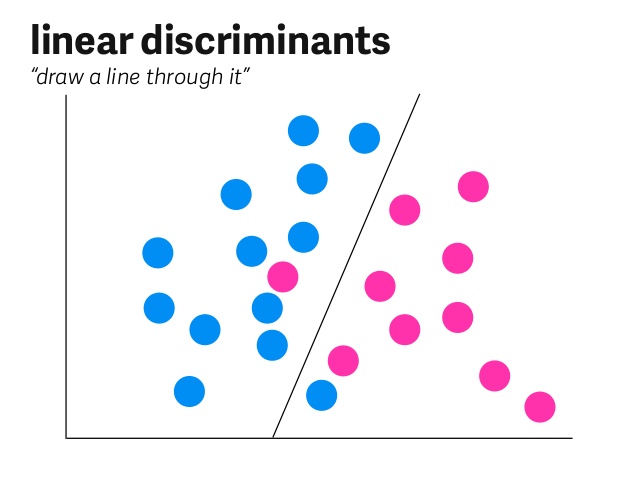
여기까지는 기존의 알고리즘을 직접 작성하는 형태와 같습니다. 등수와 시험점수를 주고, 그에 따른 중요도로 점수화한 뒤, 합산하여 일정 숫자 이상인 경우 합격이라 판단하는 것은 쉽습니다. 문제는 중요도와 편차를 모른다는 것에 있습니다.
신경망 - 가중치 찾기
앞서 말한 중요도는 신경망에선 가중치라고 표현됩니다. 사용자는 가중치와 편차를 모르므로, 신경망이 알아서 두 값을 계산해내야 합니다. 이를 계산하기 위해서, 이미 알고있는 데이터에 대하여 방정식을 세운 뒤, 예측값과 실제값을 대조하여 가중치와 편차를 다시 계산합니다. 이를 학습이라고 합니다.
실제값과 예측값이 다르면, 신경망은 이전의 가중치와 편차를 조금씩 수정합니다. 이때, 이전의 가중치와 편차를 올바르게 수정하기 위해, 확률을 사용합니다.
기존의 경우 양수는 합격(1), 음수는 불합격(0)이였습니다. 이를 예측하기 위해 신경망이 선형방정식 모델을 세우고, 예측값과 실제값을 대조한 후, 가중치와 편차를 다시 계산하였습니다. 그런데 다시 계산한 선형방정식 모델에서도 이전 모델과 같은 결과가 나온다면, 신경망이 정확한 학습을 하고 있는지 모르게 됩니다. 이를 해결하기 위해서 확률과 오류값을 도입합니다.
신경망 - 확률과 오류값
기존의 에는 양수는 합격(1), 음수는 불합격(0)이라고 하였습니다. 이젠 신경망이 정확한 학습을 하고있는지 알아보기 위해 합격, 불합격을 확률로 나타내도록 합니다. 합격할 확률이 높을수록 1에 가까워지고, 불합격할 확률이 높을수록 0에 가까워집니다. 어중간한 경우(신경망 입장에선 선형 방정식에 가까운 경우)는 0.5가 됩니다. 이를 시그모이드 함수라고 표현합니다.
이제 신경망의 정확한 학습을 확인하기 이전에, 데이터 전처리 과정이 필요합니다. 확률을 통해 현재 선형 모델이 얼마나 떨어져 있는지 확인합니다. 예를 들어, 일어날 확률이 0.7, 0.8인 두 상황이 있다고 한다면, 두 상황 모두 일어날 확률은 0.56이 됩니다. 이 값이 크면 클수록 선형모델은 더 정확하다고 판단할 수 있습니다.
이방법은 데이터가 적을땐 간단하지만, 데이터의 수가 많아지면 데이터값의 변화에 민감해 집니다. 그러니 로그를 취해 덧셈의 형식으로 나타내도록 합니다. 그후 음수를 취하도록 합니다. 이와 같은 과정을 통해 나온 수식은 다음과 같습니다.
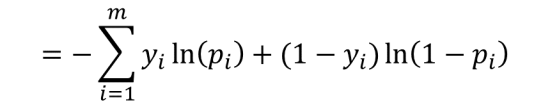
위의 식을 크로스 엔트로피라고 하며, 이 크로스 엔트로피가 작으면 작을수록 선형 모델의 신뢰도가 올라가게 됩니다.
비선형 모델
이제 선형 모델에서의 신경망형태를 알아보았습니다. 그러나 대부분의 경우는 비선형모델의 분류가 필요하게 됩니다. 이러한 비선형모델을 다음과 같이 나타낼 수 있습니다.
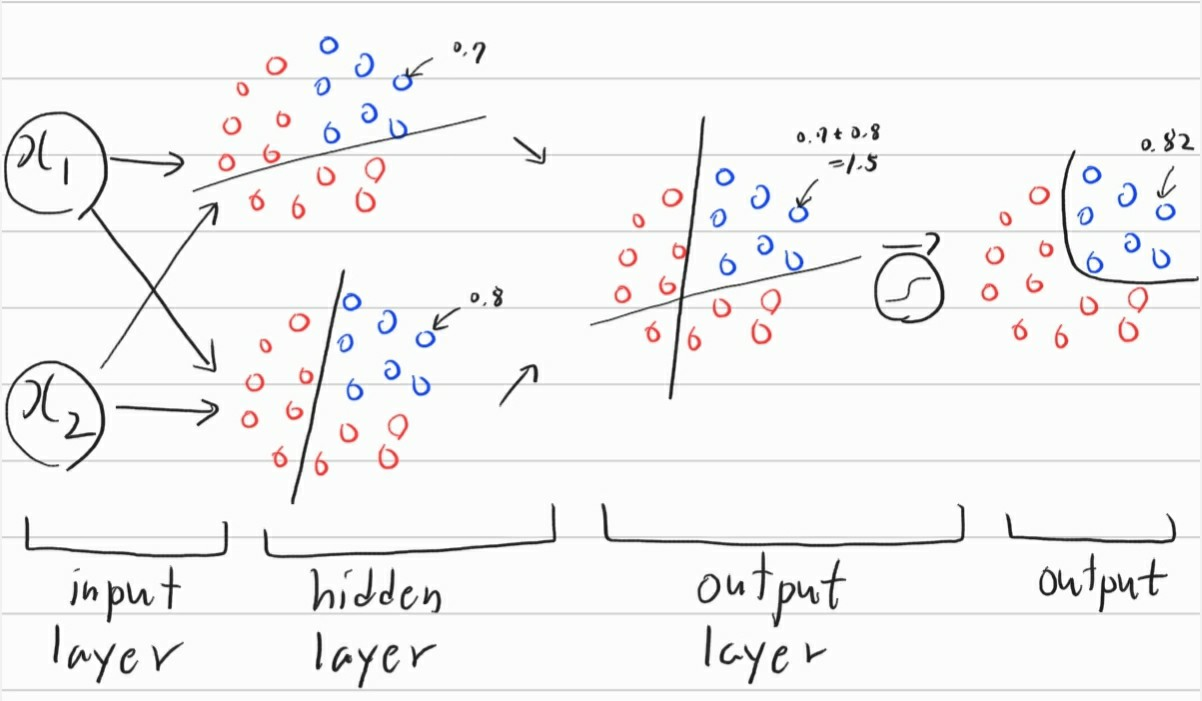
선형 모델의 신경망은 단층형태로 되어있다면, 비선형 모델은 다층형태로 되어있습니다. 신경망에서 한 층을 레이어라고 부르게 되는데, 이러한 레이어들이 다량으로 쌓이게 되고, 추정해야하는 가중치가 많아지는 경우를 딥러닝이라고 부르게 됩니다.