Advanced Computer-vision
udacity self driving car의 computer vision 부분을 통해 학습한 내용을 정리한 페이지 입니다.
개요
앞서 gradient와 조감도를 통해 차선을 추출하였습니다. 이제 추출한 차선을 통해 차량의 조향을 제어하기 위한 곡선을 추출할 차례입니다.
차선의 많은 부분은 곡선으로 되어있습니다. 이러한 곡선 도로를 주행하기 위해서는 차선의 곡률을 계산하여야 합니다. 차선의 곡률을 계산하기 위해 차선을 2차 방정식 형태로 나타내도록 합니다.
차선의 2차 방정식
차선의 2차 방정식을 구하기 위해선 차선의 위치를 찾아야 합니다. 먼저 조감도를 통해 변환한 이미지를 보도록 합니다.
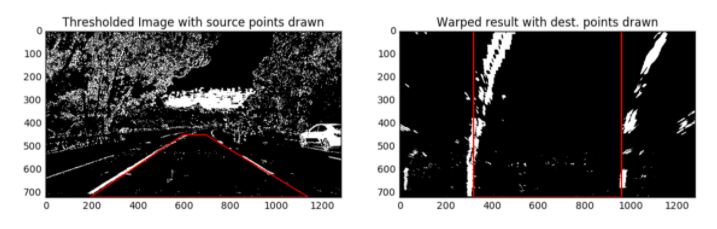
위와 같은 이미지에선 허프 변환을 통해 차선의 위치를 찾기가 어렵습니다. 그러므로 이미지의 y축을 조금씩 분할하여 차선을 찾도록 합니다.
그러기 위해선 차선이 시작되는 지점을 먼저 구해야 합니다. 이를 위해 다음 그림과 같이 이미지의 절반 중 픽셀 값이 많이 존재하는 부분을 찾도록 합니다.
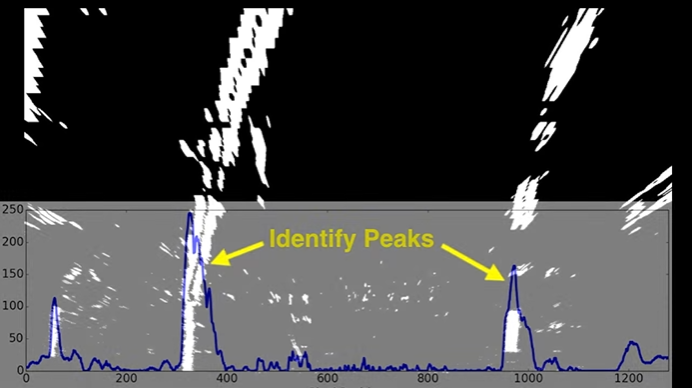
차선이 시작되는 지점을 구하였으면, 이미지의 y축을 조금씩 분할하여 차선을 찾도록 합니다. 만약 차선을 나타내는 픽셀의 평균이 왼쪽, 혹은 오른쪽으로 치우쳐져 있다면, 다음 y축에선 치우쳐진 만큼 차선 검출 픽셀의 중심을 이동시키도록 합니다.
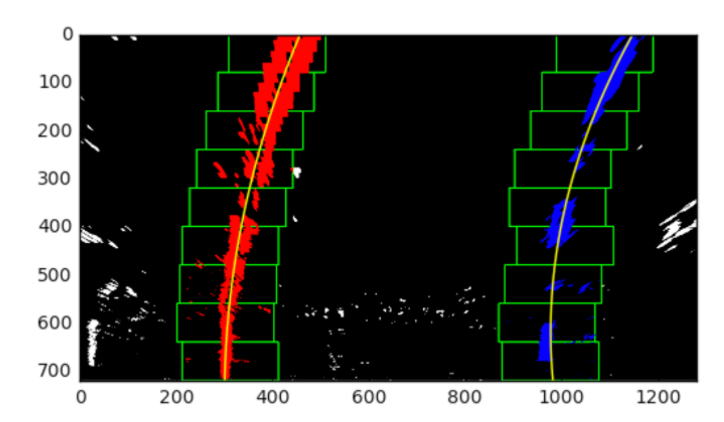
구한 차선 픽셀을 np.polyfit함수를 이용하여 2차 방정식으로 근사시키면 차선의 2차 방정식을 구할 수 있게 됩니다.
계산을 더 빠르게 하기
차선의 2차 방정식은 다음과 같이 구할 수 있지만 매 순간, 혹은 매 프레임마다 이러한 계산을 하는 것은 낭비일 수 있습니다. 계산을 간소화 하고 프로그램에 소모되는 자원을 최소화 하기 위해 또 다른 방법을 생각해볼 수 있습니다.
카메라의 프레임이 매우 낮고 매우 빠른 속도로 주행하는 자동차가 아니라면, 카메라에서 한 프레임과 그 다음프레임은 차선에서 별다른 차이가 없는 것처럼 나타납니다. 그럼 이전 프레임에서 사용하였던 차선의 2차방정식을 활용하여 다음 차선의 2차방정식을 찾아낼 수도 있습니다.
곡률 찾기

다음 그림과 같이 2차방정식을 찾았습니다. 그럼 곡률 반경을 통해 차선이 얼마나 휘어져 있는지 찾도록 합니다.
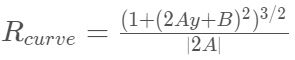
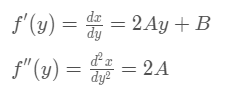
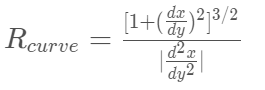
y=f(x)가 아닌 x=f(y)인 이유는 앞서 2차방정식을 찾을 때, y축을 변수로 두고 식을 찾았기 때문입니다.
곡률 반경을 찾을 때 조심해야 할것은 픽셀에서의 곡률반경이 아니라 실제 도로에서의 곡률반경을 찾아야 합니다. 그러기 위해선 실제 도로와 픽셀간의 비를 통해 계산해주어야 합니다.